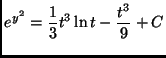(a)
![]() (b)
(b)
![]() (c)
(c)
![]() (d)
(d)
![]()
(a)
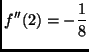 (b)
(b)
![]() (c)
(c)
![]() (d)
(d)
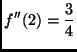
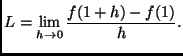
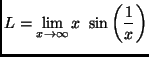 .
.
(a)
![]() (b)
(b)
![]() (c)
(c)
![]() (d)
(d)
![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a)
![]() (b)
(b)
![]() (c)
(c)
![]() (d)
(d)
![]()
(a)
![]() ,
(b)
,
(b)
![]() ,
(c)
,
(c)
![]() ,
(d)
,
(d)
![]() .
.
(a)
![]() (b)
(b)
![]() (c)
(c)
![]() (d)
(d)
![]()
(a)
![]() (b)
(b)
![]() (c)
(c)
![]() (d) None of these
(d) None of these
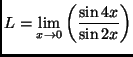 using any method.
using any method.
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d)
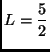
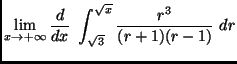
(a)
![]()
(b)
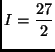
(c) This limit does not exist
(d)
![]()
(a)
![]() where
where
![]()
(b)
![]() where
where
![]()
(c)
![]() where
where
![]()
(d)
![]()
(a)
![]()
(b)
![]()
(c)
![]()
(d)
![]()
(a)
![]()
(b)
![]()
(c)
![]()
(d)
![]()
(a)
![]()
(b)
![]()
(c)
![]()
(d)
![]()
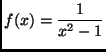 increasing?
increasing?
(a)
![]()
(b)
![]()
(c)
![]()
(d)
![]()
(a)
![]()
(b)
![]()
(c)
![]()
(d)
![]()
(a)
![]()
(b)
![]()
(c)
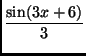
(d)
![]()
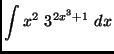
(a)
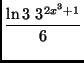
(b)
![]()
(c)
![]()
(d)
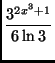
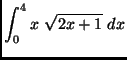
(a)
![]()
(b)
![]()
(c)
![]()
(d)
![]()
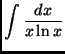 is
is
(a)
![]()
(b)
![]()
(c)
![]()
(d)
![]()
(a)
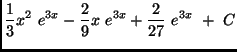
(b)
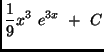
(c)
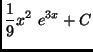
(d)
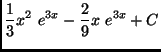
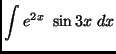 .
.
(a)
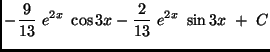
(b)
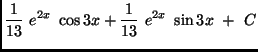
(c)
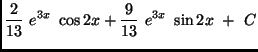
(d)
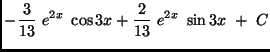
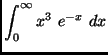 .
.
(a)
![]()
(b)
![]()
(c)
![]()
(d)
![]()
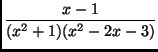
(a)
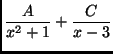
(b)
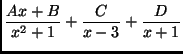
(c)
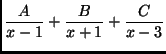
(d)
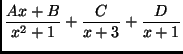
where
![]() are constants to be determined.
are constants to be determined.
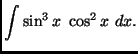
(a)
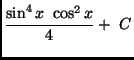
(b)
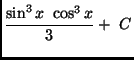
(c)
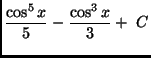
(d)
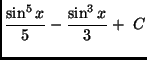
where
![]() are constants to be determined.
are constants to be determined.
(a)
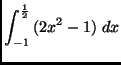
(b)
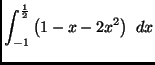
(c)
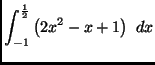
(d)
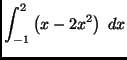
(a)
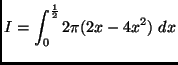
(b)
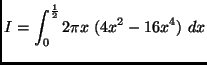
(c)
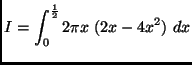
(d)
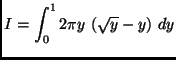
(a)
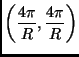
(b)
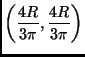
(c)
![]()
(d)

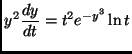
(a)
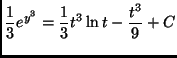
(b)
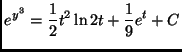
(c)
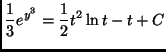 (d)
(d)